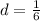Given:
The sixth term of an arithmetic sequence is
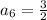
The twelfth term is
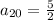
To find:
The common difference
Step-by-step explanation:
The nth term formula of an arithmetic sequence is,
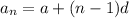
So, the sixth and twelfth terms become,
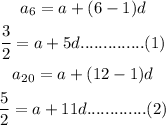
Subtract (1) from (2),
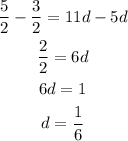
Thus, the common difference is,
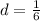
Final answer:
The common difference is,