Question

A soccer ball is kicked from an initial height of 2 feet with an upward velocity of 32 ft/s. The ball’s height, h (in feet), after t seconds is given by the following equation:h = 2 + 32t - 16t^2Find the values of t when the ball’s height is 10 feet. Round each value to the nearest hundredth.Select ALL that apply.Answer choices include: A.) 2.06 secondsB.) 0.43 secondsC.) 1.71 secondsD.) 1.43 secondsE.) 0.29 seconds

Answer 1

C.) 1.71 seconds

E.) 0.29 seconds

Explanation:

We have that the equation that models the height is the following:

`h=2+32t-16t^2`

We are asked to calculate the times when h = 10, we substitute and calculate for t, just like this:

`\begin{gathered} 10=2+32t-16t^2 \\ 32t-16t^2=10-2 \\ 32t-16t^2=8 \\ (32t)/(-16)-(16t^2)/(-16)=(8)/(-16) \\ t^2-2t+(-1)^2=-(1)/(2)+(-1)^2 \\ (t-1)^2=(1)/(2) \\ t-1=\pm\sqrt{(1)/(2)} \\ t=1\pm\sqrt{(1)/(2)} \\ t_1=1+\sqrt{(1)/(2)}=1.71\text{ sec} \\ t_2=1-\sqrt{(1)/(2)}=0.29\text{ sec} \end{gathered}`

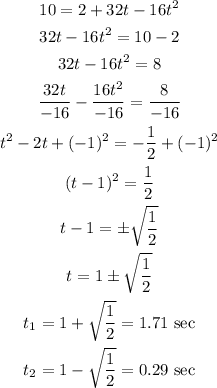
Therefore, the soccer ball has a height of 10 feet at 0.29 seconds and 1.71 seconds.