Given:
Principal(p) = $9000 rate(r) = 7% = 0.07
n=1 (number of time the interest is compounded)
a)
time (t) = 1
Using the formula;
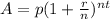
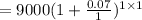
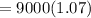
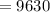
Hence, the amount owed at the end of the year is $9630
b)
t=2
Substitute the values into the formula and evaluate
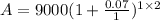
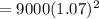
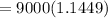
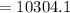
Hence, the amount owed at the end of 2 years is $10304.1