Question

a. Create a sort of complex exponential equation using a common base and solve.b. Then solve the exponential equation using logarithms.

Answer 1

We can solve a common base exponential equation of the form:

`a^(f(x))=b^(g(x))`

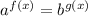
With the one-to-one property to get:

`f(x)=g(x)`

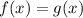
(a) In this case, we can take 4 as the common base, to get:

`4^(f(x))=4^(g(x))`

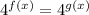
For f(x), we can use a linear equation of the form mx + b like 6x + 9, and for g(x) we can make it equal to -x² (we can use whatever equation we want because we are creating the complex exponential equation), then we get:

`4^(6x+9)=4^(-x^2)`

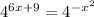
Since we have common bases, by means of the one-to-one property, we rewrite the above equation to get:

`6x+9=-x^2`

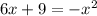
Simplifying and factoring:

6x + 9 + x² = x² - x²

6x + 9 + x² = 0

(x + 3)² = 0

Then, the solution to this equation is -3

(b) Similarly, taking logarithms on both side we get:

`\begin{gathered} Log(4^(6x+9))=Log(4^(-x^2)) \\ (6x+9)Log(4^{})=(-x^2)Log(4^{}) \end{gathered}`

By dividing both sides by Log(4), we get:

`6x+9=-x^2`

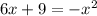
As you can see, we got the same equation as in part (a), then the solution will be the same and it is x = -3