ANSWER
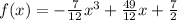
Step-by-step explanation
If x1, x2, x3, ..., xn are the zeros of a polynomial P, then the polynomial can be written as the product of the factors,
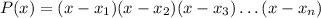
In this problem we have a third-degree polynomial function, so it has 3 zeros and thus 3 factors,
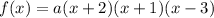
We have to find a knowing that the function has to pass through point (2, 7). This means that when x = 2, f = 7,
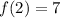
Replace into the function,
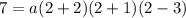
Solve the parenthesis,
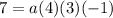
Multiply,
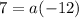
And solve for a by dividing both sides by -12,
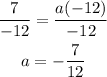
Hence, the function is
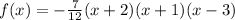
Next, we have to multiply the factors to obtain the function in standard form. Multiply the first two,
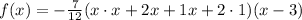
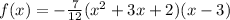
Then multiply by the last factor,
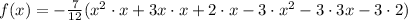
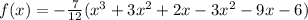
Add like terms,
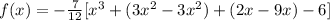
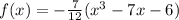
And finally, distribute the coefficient,
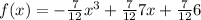
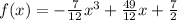
This is the polynomial function with zeros -2, -1 and 3 that passes through point (2, 7)