The area of a triangle is given by the next formula:
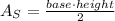
Now, in this case, we don't know the height. Therefore, we need to use Heron's formula:
![A_S=\sqrt[]{s(s-a)\cdot(s-b)\cdot(s-c)}](https://img.qammunity.org/2023/formulas/mathematics/college/7zcy3b7f7232jgmbkexikl5vskmj0auwnk.png)
Where s:
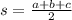
Let's find s:
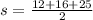
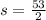
Then, replace s on the area formula:
![A=\sqrt[]{((53)/(2)((53)/(2)-12)\cdot((53)/(2)-16)\cdot((53)/(2)-25))}](https://img.qammunity.org/2023/formulas/mathematics/college/87mgymtriumbx3m95gxroqr3mue2754c3z.png)
Hence, the area of the triangle given is:
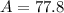
The value is rounded to the nearest tenth.