We are told that a man jumps from a plane and we are required to determine the time it takes him to reach 28.5 m/s. Since the man is falling this is a free-fall motion. In free-fall motion, the acceleration is always constant and is equivalent to the acceleration of gravity. This acceleration of symbolized with the letter "g" and its value is:
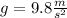
Now, to determine the time we will use the following equation of motion for an object in free-fall:
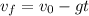
Where:
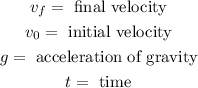
Since the man jumps from the plane the initial velocity is zero. Therefore, the equation simplifies to:

Now we solve for "t" by dividing both sides by "-g":
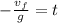
Since we need to know the time for the object to reach a velocity of 28.5 m/s, this we take as the final velocity. Since the object is falling the velocity has a negative value. Plugging in the values we get:
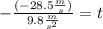
Solving the operations we get:
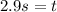
Therefore, it takes the man 2.9 seconds to reach the velocity of 28.5 m/s.