Answers:
Speed of boat in still water = 31 mph
Speed of current = 3 mph
====================================================
Step-by-step explanation:
b = speed of the boat in still water
c = speed of the current
When going with the current, the boat is sped up since the current is helping push it where it wants to go. It gets a speed boost.
The equation in this case is b+c = 34 since the boat travels 34 mph with the current.
The other equation is b-c = 28 where the current is now slowing down the boat to 28 mph.
--------------------
This is our system of equations
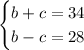
Add the equations straight down.
- The b terms add to 2b.
- The c terms cancel out (since they add to 0).
- The right hand sides add to 62.
We end up with 2b+0c = 62 or 2b = 62.
This solves to b = 31, which is the speed of the boat in still water.
Use this to find c.
b+c = 34
31+c = 34
c = 34-31
c = 3 mph is the speed of the current
Or you could say:
b-c = 28
31-c = 28
-c = 28-31
-c = -3
c = 3 mph