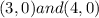
Step-by-step explanation
The zeros of a polynomial are the values of x which satisfy the equation y = f(x). Here f(x) is a function of x, and the zeros of the polynomial is the values of x for which the y value is equal to zero
so
Step 1
when the graph crosses the x-axis
let y=0
so
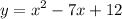
The middle number is -7 and the last number is 12.
Factoring means we want something like
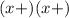
We need two numbers that...
Add together to get -7
Multiply together to get 12
so, the number are
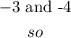
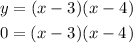
so, the solutions are
x=3
and
x=4
(3,0) and (4,0)
I hope this helps you