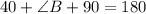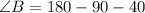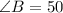Question

In the right triangle ACB, find the measure of angle (Be sure to scroll down to see all of the matching options.)DThe image shows right triangle A C B. Angle C is 90 degrees. Side A C, labeled lowercase B, is 6. Side A B is the hypotenuse. Angle A is 40degrees.ZBABCB40'5.0356.7038.99650°7.832

Answer 1

• ∠B = 50º

,

• AB = 7.832

,

• CB = 5.035

Step-by-step explanation

The triangle ABC is shown below:

As it is a right triangle, we can use trigonometric functions to solve it. To know the hypotenuse (AB), we can use the cosine function:

`\cos(x)=\frac{adjacent\text{ side}}{hypotenuse}`

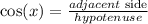
In our case, the adjacent side is b and the hypotenuse is AB. Then, by replacing our expressions we get:

`\cos(A)=(b)/(AB)`

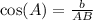
Next, by replacing the values and solving for AB we get:

`\cos(40\degree)=(6)/(AB)`
`AB=(6)/(\cos(40\degree))`
`AB\approx7.832`

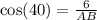
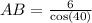
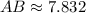
As we have two sides, we can use the Pythagorean Theorem to find side CB:

`AB^2=b^2+CB^2`
`AB^2=b^2+CB^2`

Next, we can solve for CB (the side that we are lacking) as follows:

`CB=√(AB^2-b^2)`
`CB=√(7.832^2-6^2)`
`CB=√(7.832^2-6^2)\approx5.035`

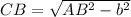
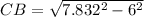
Finally, as the addition of the interior angles of a triangle adds up to 180º, we can find ∠B as follows:

`\angle A+\angle B+\angle C=180\degree`
`40\degree+\angle B+90\degree=180\degree`
`\angle B=180\degree-90\degree-40\degree`
`\angle B=50\degree`