The gravitational force acting on the mass can be given as,
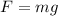
The spring constant of the spring can be given as,
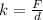
Substitute the known expression,

Substitute the known values,
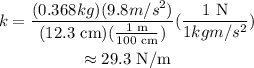
The work done on the spring can be given as,
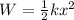
Substitute the known values,
![\begin{gathered} 0.399J=(1)/(2)(29.3N/m)x^2 \\ x^2=\frac{2(0.399\text{ J)}}{29.3\text{ N/m}}(\frac{1\text{ Nm}}{1\text{ J}}) \\ x=\sqrt[]{0.0272m^2} \\ \approx0.165\text{ m} \end{gathered}](https://img.qammunity.org/2023/formulas/physics/college/812umh7ryob55jwq7ecko7klwpxypwo0vz.png)
Thus, the distance of spring stretched is 0.165 m.