The transformation we need is:
Translate triangle A 1 unit up and 1 unit to the left, rotate it 90° clockwise about the origin, and reflect it over the y-axis. Therefore the answer is C.
This comes from the following facts.
A translation 1 unit up and 1 unit to the left is given by:
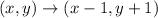
Then the original vertexes take the form:
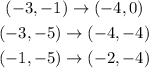
Now, we make a rotation of 90° clockwise, this is given by:
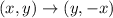
Then we have:
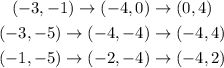
Finally we make a reflection over the y-axis, this is given by:
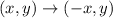
Then we have:
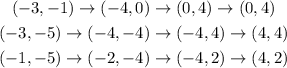
Therefore the whole transformation is:
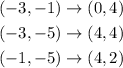
And we notice that this transformation takes triangle A onto triangle B.