Question

Juana weighed a sample of 121212 jumbo eggs. Here are their weights (in grams):

Answer 1

If a variable X has taken n values and its mean is X' then the standard deviation is given by

`s\text{d}=\sqrt[]{((X_1-X^(\prime))^2+(X_2-X^(\prime))^2+\cdots+(X_n-X^(\prime))^2)/(n-1)}`

Given data:

It is given that that there are 12 eggs and there weights are

`\begin{gathered} 67,67,68,69,69,70 \\ 71,71,71,72,72,73 \end{gathered}`

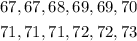
and there mean weight is 70 grams.

So n=12 and X'=70

So, standard deviation will be

`\begin{gathered} sd=\sqrt[]{((67-70)^2+(67-70)^2+\cdots+(73-70)^2)/(12-1)} \\ sd=\sqrt[]{((67-70)^2+(67-70)^2+\cdots+(73-70)^2)/(11)} \end{gathered}`

So, the correct option is A.