Question

Help with algebra 2 question State the first four terms of sequence

Answer 1

`\begin{gathered} a_1=3 \\ a_n=1+2a_(n-1) \end{gathered}`

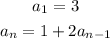
Then we have:

`\begin{gathered} a_2=1+2a_1=1+2\cdot3=7 \\ a_3=1+2a_2=1+2\cdot7=15 \\ a_4=1+2a_3=1+2\cdot15=31 \\ a_5=1+2a_4=1+2\cdot31=63 \end{gathered}`

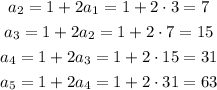
This sequence isn't either arithmetic or geometric

A geometric sequence is the one which every term ahead of the first one is resulted from the product of the previous term by a constant number.

In this case, this sequence is not exactly a geometric sequence by we add +1 to the product of the previous term and 2.