Question

A regular polygon has a side length of 4.8 cm, an apothem of 7.4 cm and an area of177.6 sq. cm. Find the number of sides this regular polygon has.

Answer 1

The area of a regular polygon is determined by the formula

`\begin{gathered} A=(1)/(2)ap \\ \text{where} \\ a\text{ is the apothem} \\ p\text{ is the perimeter} \end{gathered}`

The perimeter of a regular polygon is

`\begin{gathered} p=n\cdot s \\ \text{where} \\ n\text{ is the number of sides} \\ s\text{ is the side length} \end{gathered}`

Given that the apothem is 7.4 cm, side length is 4.8 cm, and the area is 177.6 sq cm, substitute these to the formula for area and we have

`\begin{gathered} A=(1)/(2)ap \\ 177.6\text{ cm}^2=(1)/(2)\cdot7.4\text{ cm}\cdot(4.8\text{ cm}\cdot n) \\ 177.6\text{ cm}^2=(3.7\text{ cm})\cdot(4.8n\text{ cm}) \\ 177.6\text{ cm}^2=17.76n\text{ cm}^2 \\ \frac{177.6\text{ cm}^2}{17.76\text{ cm}^2}=\frac{17.76n\text{ cm}^2}{17.76\text{ cm}^2} \\ 10=n \\ n=10 \end{gathered}`

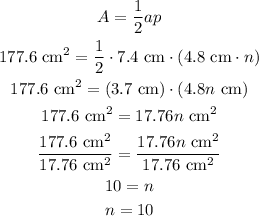
Therefore, the number of sides of the given regular polygon is 10.