Question

a 20 foot string of lights is attached to the top of a 12-foot pole for a holiday display. How far from the base of the pole should the end be anchored?

Answer 1

Step 1: Problem

a 20 foot string of lights is attached to the top of a 12-foot pole for a holiday display. How far from the base of the pole should the end be anchored?​

Step 2: Concept

Draw a diagram to illustrate the question.

Step 3: Method

`\begin{gathered} \text{Apply pythagoras theorem to find how far from the base of the pole is the end of } \\ \text{the string light} \\ \text{Opposite}^2+Adjacent^2=Hypotenuse^2 \end{gathered}`

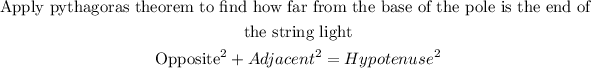
Opposite = 12

Adjacent = L

Hypotenuse = 20

`\begin{gathered} \text{Opposite}^2+Adjacent^2=Hypotenuse^2 \\ 12^2+L^2=20^2 \\ 144+L^2\text{ = 400} \\ \text{Collect like terms} \\ L^2\text{ = 400 - 144} \\ L^2\text{ = 256} \\ L\text{ = }\sqrt[]{256} \\ L\text{ = 16 foot} \end{gathered}`

Step 4: Final answer

The end of the string light from the base of the pole = 16 foot

Final answer = 16 foot