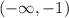Question

Explain how the graph of the function f(x) =-3 can be obtained from the graph of y=- Then graph fand(x + 1)²give the (a) domain and (b) range. Determine the largest open intervals of the domain over which the function is (c)increasing or (d) decreasing.To obtain the graph of f, shift the graph of y=-1 unit, reflect across theand shift 3 units

Answer 1

Parent function:

`y=(1)/(x^2)`

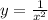
Transformations:

`\begin{gathered} y=(-a1)/((x\pm h)^2)\pm k \\ \\ -a:reflection\text{ }across\text{ }x-axis \\ +h:translation\text{ }h\text{ }units\text{ }to\text{ }the\text{ }left \\ -h:translation\text{ }h\text{ }units\text{ }to\text{ }the\text{ }right \\ +k:translation\text{ }k\text{ }units\text{ }up \\ -k:translation\text{ }k\text{ }units\text{ }down \end{gathered}`

To get function f:

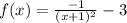
`f(x)=(-1)/((x+1)^2)-3`To obtain the graph of f, shift (translated) graph of y to the left 1 unit, reflect across the x-axis and shift 3 units down.

Graph of y:

Graph of f; on the graph above use the transformations described above to get the graph of f(x):

y in blue

f(x) in green

For f:

a) domain: x-values for which it is defined, f is defined for all x except for x-1

Domain:
`(-\infty,-1)\cup(-1,\infty)`

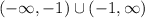
b) range: values taht takes the function, function takes values less than -3

Range:
`(-\infty,-3)`

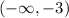
c) the function is increasing from -1 to infinite

`(-1,\infty)`

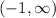
d) the function is decreasing from - infinite to -1:

`(-\infty,-1)`