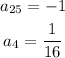Given-
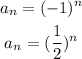
=Required- To find out the following,
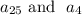
Explanation- For finding the value of
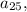
Putting n=25 in our given sequence we get,
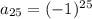
Since, odd power to a negative number gives a negative result. Hence,
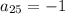
For the second part,
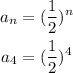
which on further solving gives,
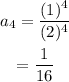
Final Answer-