SOLUTION
Given the question in the image, the following are the solution steps to answer the question.
STEP 1: Explain the concept
Tossing a coin, Sample space (S) = {H,T}
Total outcome n(S) = 2
Probability =
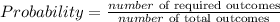
Conditional probablity: P(A|B) =
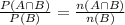
STEP 2: Calculate the probability
A fair coin tossed three times will have the sample space (S) given as:
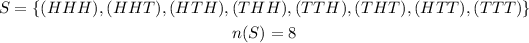
Let, event for getting at least two tails is A
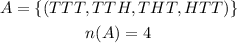
Let, event for getting at least one tail is B
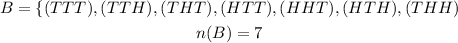
Now,
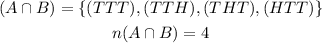
The answer is therefore calculated as:
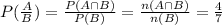
Hence, the answer is 4/7