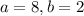Question

9. The lengths of the rectangle are labeled below. Solve for a and b.

Answer 1

Statement Problem: Solve for a and b in the rectangle given below;

Solution:

The opposite sides of a rectangle is equal. Hence,

`\begin{gathered} 2a+7b=30\ldots.\ldots\ldots\ldots\text{.equation 1} \\ 3a-2b=20\ldots\ldots\ldots\ldots\text{.equation 2} \end{gathered}`

Then, we would solve equation 1 and equation simultaneously.

Next, multiply equation 1 by 3 and equation 2 by 2, then subtract to eliminate a, we have;

`\begin{gathered} 2a+7b=30\ldots.\ldots\ldots*3 \\ 3a-2b=20\ldots\ldots\ldots*2 \\ 6a+21b=90\ldots\ldots\ldots.equation3 \\ 6a-4b=40\ldots\ldots.\ldots.equation4 \\ equation3-equation4; \\ 6a-6a+21b-(-4b)=90-40 \\ 25b=50 \\ \text{Divide both sides by 25;} \\ (25b)/(25)=(50)/(25) \\ b=2 \end{gathered}`

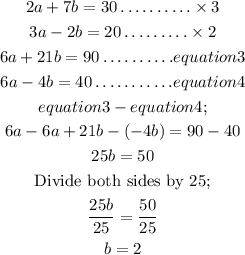
Then, substitute the value of b in equation 1 to solve for a.

`\begin{gathered} 2a+7b=30 \\ 2a+7(2)=30 \\ 2a+14=30 \\ 2a=30-14 \\ 2a=16 \\ \text{Divide both sides by 2;} \\ (2a)/(2)=(16)/(2) \\ a=8 \end{gathered}`

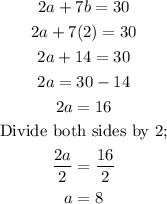
Hence, the value of a and b is;

`a=8,b=2`