Question

Suppose A is in quadrant 2 and B is in Quadrant 2

Answer 1

Given that:

`\cos(A)=-(9)/(41),\text{ }\sin(B)=(63)/(65)`

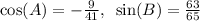
To evaluate sin (A+B) and sin (A-B),

Step 1: Express the compound angle formula.

According to the compound angle formula,

`\begin{gathered} \sin(A+B)=\sin(A)\cos(B)+\sin(B)\cos(A) \\ \sin(A-B)=\sin(A)\cos(B)-\sin(B)\cos(A) \end{gathered}`

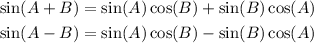
Step 2: Evaluate cos (B) and sin (A).

According to the Pythagorean identities,

`\cos^2\theta+sin^2\theta=1`

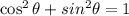
Thus,

`\begin{gathered} \sin^(A)=√(1-\cos^2A)\text{ =}\sqrt{1-(-(9)/(41))^2} \\ =\sqrt{1-(81)/(1681)} \\ =\sqrt{(1600)/(1681)} \\ \Rightarrow\sin^(A)=(40)/(41) \end{gathered}`

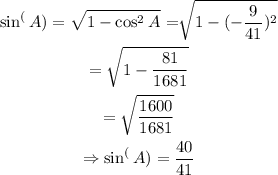
Similarly,

`\begin{gathered} \cos(B)=√(1-\sin^2B)\text{ =}\sqrt{1-((63)/(65))^2} \\ =\sqrt{1-(3969)/(4225)} \\ =\sqrt{(256)/(4225)} \\ \Rightarrow\cos(B)=-(16)/(65)\text{ \lparen second quadrant\rparen} \end{gathered}`

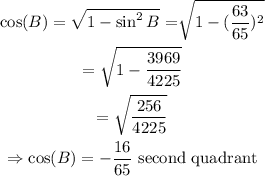
Step 3: Evaluate sin (A+B).

Recall,

`\begin{gathered} \sin(A+B)=\sin(A)\cos(B)+\sin(B)\cos(A) \\ =((40)/(41)*-(16)/(65))+((63)/(65)*-(9)/(41)) \\ =-(1207)/(2665) \end{gathered}`

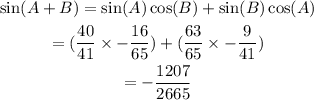
Step 4: Evaluate sin(A-B).

Recall,

`\begin{gathered} \sin(A-B)=\sin(A)\cos(B)-\sin(B)\cos(A) \\ =((40)/(41)*-(16)/(65))-((63)/(65)*-(9)/(41)) \\ =-(73)/(2665) \end{gathered}`

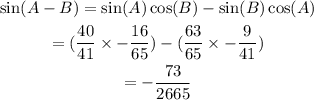
Hence, we have