Question

The profit from the production and sale of specialty golf hats is given by the function P(x)=20x−7000 where x is the number of hats produced and sold.(a) Producing and selling how many hats will give a profit of $7000?(b) How many hats must be produced and sold to avoid a loss?

Answer 1

`p(x)=20x-7000`

where:

x = the number of hats

p(x) = profit

To solve how many hats must be produced and sold to have a profit of $7 000, let's replace p(x) with $7 000.

`7,000=20x-7000`

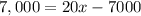
The next step is to isolate the term with the variable "x" on one side. For this to happen, let's add 7,000 on both sides of the equation.

`\begin{gathered} 7,000+7,000=20x-7,000+7,000 \\ 14,000=20x \end{gathered}`

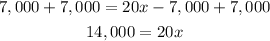
The last step is to divide both sides of the equation by 20 to solve x.

`\begin{gathered} (14,000)/(20)=(20x)/(20) \\ 700=x \end{gathered}`

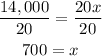
Therefore, 700 hats must be produced and sold to gain a profit of $7,000.

In order to avoid loss, the profit must be either zero or greater than that. To determine the least number of hats to be produced and sold to avoid loss, let's replace p(x) = 0.

`0=20x-7000`

Same process: Isolate the term with a variable "x" on one side. To do this, add 7000 on both sides of the equation.

`\begin{gathered} 0+7000=20x-7000+7000 \\ 7000=20x \end{gathered}`

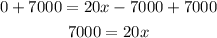
Last step, divide both sides of the equation by 20.

`\begin{gathered} (7000)/(20)=(20x)/(20) \\ 350=x \end{gathered}`

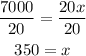
Therefore, to avoid loss, they must produce and sell at least 350 hats.