Question

Calculate the [OH-] and [H3O+] for 0.00016 M NaOH. Answer in units of M for both answers.

Answer 1

The question requires us to calculate the concentration, in mol/L, of H3O+ and OH- ions for a 0.00016 M NaOH solution.

Since NaOH is a strong base, we can consider that it completely dissociates in water:

`NaOH_((aq))\to Na^+_((aq))+OH^-_((aq))`

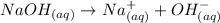
From the dissociation reaction shown above, we can say that the concentration of OH- ions in a NaOH solution will be the same as the concentration of NaOH.

Thus: [OH-] = 0.00016 mol/L

Now, we can apply the ion-product constant of liquid water (Kw) to calculate the concentration of H3O+ ions:

`\begin{gathered} K_{w_{}}=\lbrack H_3O^+\rbrack*\lbrack OH^-\rbrack \\ \lbrack H_3O^+\rbrack=(K_w)/(\lbrack OH^-\rbrack) \end{gathered}`

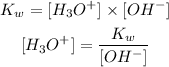
Since the value of [OH-] is 0.00016 M and considering the value of Kw as 1.00 x 10^-14, we calcuate [H3O+]:

`\lbrack H_3O^+^{}\rbrack=(1.00*10^(-14))/(0.00016)=6.3*10^(-11)mol/L`

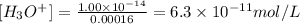
Therefore, the concentration of [OH-] and [H3O+] ions are 1.6 x 10^-4 and 6.3 x 10^-11 M, respectively.