Question

Use the functions f(x) =x^ 2 -3 and g(x) = 2x- 1. Find each of the following, What is (f+g) (2) ? What is (f/g) (-1) What is the domain of (f.g)(x)

Answer 1

Given the functions

`\begin{gathered} f(x)=x^2-3 \\ g(x)=2x-1 \end{gathered}`

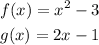
PART 1:

Concept:

`(f+g)(x)=f(x)+g(x)`

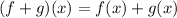
By applying the rule above, we will have

`\begin{gathered} (f+g)(x)=f(x)+g(x) \\ (f+g)(x)=x^2-3+2x-1 \\ (f+g)(x)=x^2+2x-3-1 \\ (f+g)(x)=x^2+2x-4 \end{gathered}`

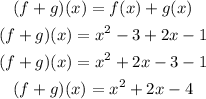
To figure out (f+g)(2) means that we are going to substitute the value of x as 2

`\begin{gathered} (f+g)(x)=x^2+2x-4 \\ (f+g)(2)=2^2+2(2)-4 \\ (f+g)(2)=4+4-4 \\ (f+g)(2)=4 \end{gathered}`

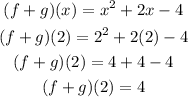
Hence,

(f+g)(2) = 4

PART 2:

Concept:

`((f)/(g))(x)=(f(x))/(g(x))`

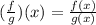
By applying the rule above, we will have

`\begin{gathered} ((f)/(g))(x)=(f(x))/(g(x)) \\ ((f)/(g))(x)=(x^2-3)/(2x-1) \end{gathered}`

To figure out the value of (f/g)(-1) means we will substitute the value of x=-1

`\begin{gathered} ((f)/(g))(x)=(x^2-3)/(2x-1) \\ ((f)/(g))(-1)=((-1)^2-3)/(2(-1)-1) \\ ((f)/(g))(-1)=(1-3)/(-2-1) \\ ((f)/(g))(-1)=(-2)/(-3) \\ ((f)/(g))(-1)=(2)/(3) \end{gathered}`

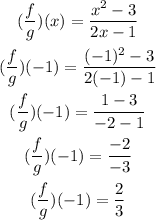
Hence,

(f/g)(-1) = 2/3

PART 3:

To figure out the domain of (f.g)(x)

`(f.g)(x)=f(x)\text{.g(x)}`

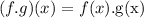
By applying the formula above, we will have

`\begin{gathered} (f.g)(x)=f(x)\text{.g(x)} \\ (f.g)(x)=(x^2-3)(2x-1) \\ (f.g)(x)=x^2(2x-1)-3(2x-1) \\ (f.g)(x)=x^3-x^2-6x+3 \end{gathered}`

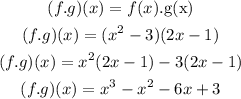
Hence,

The domain of the above set of equations is given below as

[tex]=\quad \begin{bmatrix}\mathrm{Solution\colon}\: & \: -\infty\: