The given equation is

to find the second derivative.
for that let us find the first derivative,
use the formula,
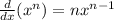
apply the chian rule,
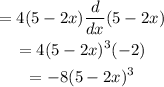
Now, let us find the second derivative.

take out the constant,
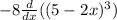
use the formula,
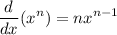
apply the chain rule,

the answer is
