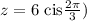Solution:
A complex number of the form:

is expressed in polar form as
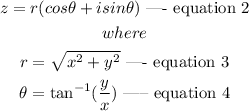
Given the complex number:
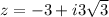
This implies that
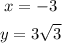
To express in polar form as shown in equation 2,
step 1: Evaluate the value of r.
From equation 3,
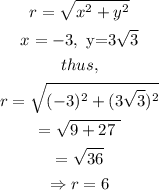
step 2: Evaluate the positive value of θ.
From equation 4,
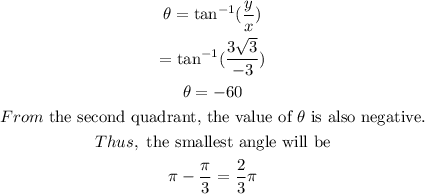
step 3: Substitute the values of r and θ into equation 2.
Thus,

Thus, the polar form of the complex number is expressed as