Question

An initial population of 750 endangered turtles triples each year for 5 years.• Write an exponential growth function to model the situation.• Find the population after 5 years.Blank 1:Blank 2:Question 7 (1 point)A car bought for $13,000 depreciates at 12% per annum. What is its value after 7 years?

Answer 1

Question 6

Blank 1

`y=750*3^x`

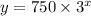
exponential fuction to represent the number of turtles, 750 is initial amount and 3 the growth per year

x the number of years

then replace x=5 to fint eh number of turtles

`\begin{gathered} y=750*3^5 \\ \\ y=750*243 \\ y=182250 \end{gathered}`

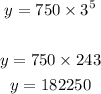
Blank 2

the population after 5 years is 182,250 turtles

Question 7

if it loses its value by 12% it means that it is only worth 88%

this percentage should be represented divided into 100

`(88)/(100)=0.88`

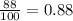
so the car is worth 88% of its initial value every year

the equation

blank1

`y=13000*(0.88)^x`

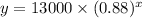
where 13000 is the initial value, 0.88 the annual decrease and x th enumber of years

Blank 2

replace x=7

`\begin{gathered} y=13000*(0.88)^7 \\ y=13000*(0.4087) \\ \\ y=5312.78 \end{gathered}`

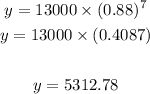
the value after 7 years is $5,312.78