Step 1
Given;
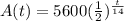
Required; To find the amount A(t) of a sample of uranium-240 remaining (in grams) after 13 hours and 60 hours
Step 2
Find the initial amount. To do this we set t=0
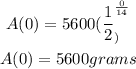
Hence the equation remains valid
Step 3
Find the amount A(t) left after 13 hours
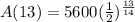
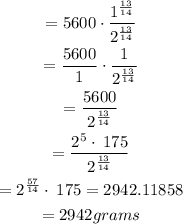
Step 4
Find the amount A(t) left after 60 hours
![\begin{gathered} A(60)=5600((1)/(2))^^{(60)/(14)} \\ =5600\cdot \frac{1^{(60)/(14)}}{2^{(60)/(14)}} \\ =5600\cdot \frac{1}{2^{(60)/(14)}} \\ =(5600)/(1)\cdot \frac{1}{16\cdot \:2^{(2)/(7)}} \\ =\frac{5600}{16\cdot \:2^{(2)/(7)}} \\ =\frac{16\cdot \:350}{16\cdot \:2^{(2)/(7)}} \\ =\frac{350}{2^{(2)/(7)}} \\ =2^{(5)/(7)}\cdot \:175 \\ A(60)=287.11737 \\ A(60)\approx287grams \end{gathered}]()
Answers;
