Question

How do i do direct variations proportions

Answer 1

In order to explain how to do direct variations proportions, let's use the following example:

"Two apples have a cost of $3. So what is the cost of six apples?"

In this problem, if the number of apples increase, the cost also increases (in the same proportion), so we have a direct variation proportion.

The proportion of the cost and the number of apples is always the same, so we can write:

`\begin{gathered} \frac{\text{ cost1}}{\text{ number1}}=\frac{\text{ cost2}}{\text{ number2}} \\ (3)/(2)=(x)/(6) \end{gathered}`

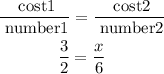
Where x represents the cost we want to find. So after writing this equation with fractions, we can solve for x:

`\begin{gathered} 3=(2\cdot x)/(6) \\ 3=(x)/(3) \\ x=3\cdot3 \\ x=9 \end{gathered}`

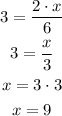
So the final cost for six apples is $9.