we are given the following formula for the balance of a bank account:
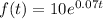
a. The opening balance is given when the value of the time "t" is zero, that is t = 0:
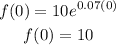
Therefore, the initial balance is 10.
b. To determine when the balance reaches 1000000 we need to replace f(t) = 1000000 and solve for "t":
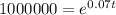
Taking natural logarithm on both sides:
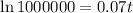
Dividing both sides by 0.07:

Solving the operation:
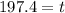
Therefore, the balance will be 1000000 in 197.4 years.