Question

9) Yilmer works at a camera store. He earns a guaranteed salary each week. In additionto his guaranteed salary, he earns a commission for each camera he sells. The graph shows his weekly pay as a function of how many cameras he sells during theweek. Which equation can be used to calculate how much Yilmer earns each week? Let P represent his weekly pay and let c represent the number of cameras he sells.

Answer 1

To find the equation that models the situation, we just have to calculate the equation of the line.

To do so, we'll use points (2, 160) and (4, 200). First, let's calculate the slope:

`m=(200-160)/(4-2)\rightarrow m=20`

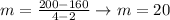
Now, let's use this slope, point (2, 160) and the slope intercept form to calculate an equation for the line:

`\begin{gathered} y-160=20(x-2)\rightarrow y-160=20x-40 \\ \end{gathered}`

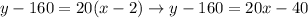
Clearing y to get the slope-intercept form,

`\rightarrow y=20x+120`

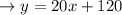
Notice y is the weekly salary, and x is the cameras sold. Thereby,

`P=20c+120`

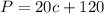
(Correct answer: Option 3)