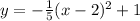ANSWER:
(2, 1)
Step-by-step explanation:
Given:
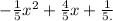
To find:
The vertex of the function
Step-by-step solution:
To be able to determine the vertex of the given function, we have to rewrite the function in the below vertex form;

where (h, k ) is the vertex of the function.
Recall that a quadratic equation in general form is given as;

If we compare the above equation with the given equation, we see that a = -1/5, b = 4/5, and c = 1/5
We'll find the value of h using the below formula;
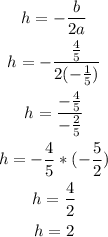
We can now determine the value of k as seen below;
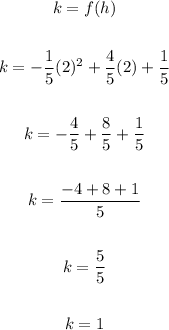
Since h = 2 and k = 1, then the vertex of the function is (2, 1) and we can write the function in vertex form as;