Question

.) A florist wishes to make bouquets of mixed spring flowers. Each bouquet is to be made up of tulips at $10 a bunch and daffodils at $7 a bunch. How many bunches of each should she use to make 15 bunches which she can sell for $8 a bunch? 2.). If an alloy containing 30% silver is mixed with a 55% silver alloy to get 800 pounds of 40% alloy, how much of each must be used?

Answer 1

We have the following:

1.

let x a tulips

let y daffodils

therefore:

`\begin{gathered} x+y=15\rightarrow x=15-y \\ 10x+7y=(x+y)8\rightarrow10x+7y=120 \end{gathered}`

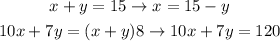
solving:

`\begin{gathered} 10\cdot(15-y)+7y=120 \\ 150-10y+7y=120 \\ 10y-7y=150-120 \\ 3y=30 \\ y=(30)/(3)=10 \end{gathered}`

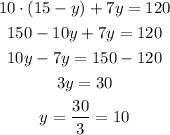
for x:

`x=15-10=5`

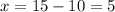
Therefore, the answer is 5 tulips and 10 daffodils

2.

let x a 30% silver

let y a 55% silver

`\begin{gathered} x+y=800\rightarrow x=800-y \\ 30x+55y=40\cdot(x+y)\rightarrow30x+55y=32000 \end{gathered}`

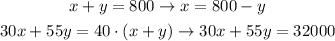
solving:

`\begin{gathered} 30\cdot(800-y)+55y=32000 \\ 24000-30y+55y=32000 \\ 25y=32000-24000 \\ y=(8000)/(25) \\ y=320 \end{gathered}`

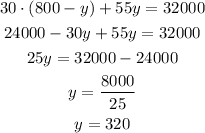
for x:

`x=800-320=480`

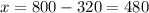
Therefore, the answer is 480 pounds of 30% silver and 320 pounds of 55% silver