Question

Sketch a graph of the following functions. Label at least one key point.a) f(x) = V- (x + 3) -2.b) g(x) =- (x - 1)2 + 5

Answer 1

a. The given function is:

`f(x)=\sqrt[]{-(x+3)}-2`

It has a restriction in the domain given that the radicand of the square root can't be negative. Then:

`\begin{gathered} -(x+3)\ge0 \\ x+3\le0 \\ x\le-3 \end{gathered}`

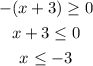
Then, we can start with x=-3:

`\begin{gathered} f(-3)=\sqrt[]{-(-3+3)}-2 \\ f(-3)=\sqrt[]{-(0)}-2 \\ f(-3)=\sqrt[]{0}-2 \\ f(-3)=-2 \end{gathered}`

The first point is (-3,-2)

Now, x=-4:

`\begin{gathered} f(-4)=\sqrt[]{-(-4+3)}-2 \\ f(-4)=\sqrt[]{-(-1)}-2 \\ f(-4)=\sqrt[]{1}-2 \\ f(-4)=1-2 \\ f(-4)=-1 \end{gathered}`

The second point is (-4,-1)

And now we can evaluate f(-7):

`\begin{gathered} f(-7)=\sqrt[]{-(-7+3)}-2 \\ f(-7)=\sqrt[]{-(-4)}-2 \\ f(-7)=\sqrt[]{4}-2 \\ f(-7)=2-2 \\ f(-7)=0 \end{gathered}`

Another point in the graph is (-7,0).

Let's evaluate a last point f(-10):

`\begin{gathered} f(-10)=\sqrt[]{-(-10+3)}-2 \\ f(-10)=\sqrt[]{-(-7)}-2 \\ f(-10)=\sqrt[]{7}-2 \\ f(-10)=2.646-2 \\ f(-10)=0.646 \end{gathered}`

Now, the sketch of the graph will be:

b. The function is:

`g(x)=-(x-1)^2+5`

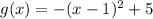
This has no restrictions in the domain.

Let's evaluate g(0):

`\begin{gathered} g(0)=-(0-1)^2+5_{}_{} \\ g(0)=-(-1)^2+5_{} \\ g(0)=-1+5_{} \\ g(0)=4 \end{gathered}`

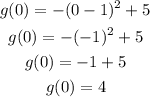
The first point is (0,4).

Now, g(1):

`\begin{gathered} g(1)=-(1-1)^2+5_{} \\ g(1)=-(0)^2+5_{} \\ g(1)=-0+5_{} \\ g(1)=5_{} \end{gathered}`

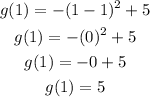
The second point is (1,5).

Evaluate g(3):

`\begin{gathered} g(3)=-(3-1)^2+5_{} \\ g(3)=-(2)^2+5_{} \\ g(3)=-4+5_{} \\ g(3)=1 \end{gathered}`

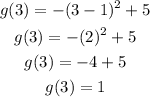
The third point is (3,1).

And evaluate g(-1):

`\begin{gathered} g(-1)=-(-1-1)^2+5_{} \\ g(-1)=-(-2)^2+5_{} \\ g(-1)=-4+5_{} \\ g(-1)=1 \end{gathered}`

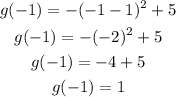
Another point is (-1,1).

The sketch of the graph will look like this: