We can evaluate the six trigonometric functions for t = -7π/4.
First, we start by transforming it into a positive angle, adding a full circle (2π):
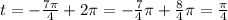
Now, we can evaluate the basic 3 trigonometric functions as:
![\begin{gathered} \sin (t)=\frac{\sqrt[]{2}}{2} \\ \cos (t)=\frac{\sqrt[]{2}}{2} \\ \tan (t)=(\sin(t))/(\cos(t))=\frac{\frac{\sqrt[]{2}}{2}}{\frac{\sqrt[]{2}}{2}}=1 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/sva4bhlag9swvguibpuztenvb78phebhao.png)
and the other 3 can be evaluated as:
![\begin{gathered} \csc (t)=(1)/(\sin(t))=\frac{2}{\sqrt[]{2}}\cdot\frac{\sqrt[]{2}}{\sqrt[]{2}}=\frac{2\sqrt[]{2}}{2}=\sqrt[]{2} \\ \sec (t)=(1)/(\cos(t))=\sqrt[]{2} \\ \cot (t)=(1)/(\tan (t))=1 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/ah7uvt9vfpip01edf5qtp27jbxr6g1vxed.png)
Answer: if t = -7π/4, we have
sin(t) =√2/2
cos(t) = √2/2
tan(t) = 1
csc(t) =√2
sec(t) =√2
cot(t) = 1