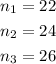Question

Help me with my Class Work can you help me with 2-A

Answer 1

We are asked to determine three consecutive even numbers such that twice the first is 20 more than the second. Let "x" be the first number, therefore, we have:

`\begin{gathered} n_1=x \\ n_2=x+2 \\ n_3=x+4 \end{gathered}`

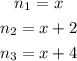
Where:

`n_(1,)n_2,n_3=\text{ first, second, and third numbers}`

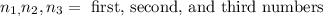
According to the condition given we have:

`2n_1=n_2+20`

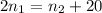
Now, we substitute for the numbers in terms of "x":

`2x=x+2+20`

Adding like terms:

`2x=x+22`

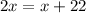
Now, we subtract "x" from both sides:

`\begin{gathered} 2x-x=x-x+22 \\ x=22 \end{gathered}`

Therefore, the first number is 22. The second and third numbers are then:

`\begin{gathered} n_1=22 \\ n_2=24 \\ n_3=26 \end{gathered}`