Sam is making a pennant in the shape of a triangle for his senior class photo. He wants the base length of this triangle to be 8 inches. The area of the pennant must be at most 20 square inches. (Sam doesn't want to buy more materials.) Write an inequality that describes the possible heights (in Inches) of the triangle. Use h for the height of the triangular pennant.
we know that
The area of triangle is equal to
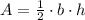
we have in this problem
b=8 in
at most -----> is less than or equal to
so
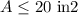
substitute
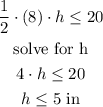
therefore
the height must be less than or equal to 5 inches