Question

Membership warehouse clubs offer shoppers low prices, along with rewards of cash back on club purchases. If the yearly fee for a warehouse club membershipis $100 and the reward rate is 4% on club purchases for the year, then the linear equation y=100-0,04x models the actual yearly cost of the membership y, indollars. Here x represents the yearly amount of club purchases, also in dollars.a) Determine the actual yearly cost of the membership if club purchases for the yearare $2100b) What amount of club purchases would reduce the actual yearly cost of the membershipto $47c) How much would a member have to spend in yearly club purchases to reduce theyearly membership cost to $0?a) The actual yearly cost of the membership if club purchases for the year are $2100 is $(Simplify your answer. Type an integer or a decimal.)

Answer 1

Given:

yearly fee for a warehouse club membership = $100

reward rate = 4% on club purchases for the year

The linear equation that models the actual yearly cost of the membership:

`\begin{gathered} y\text{ = 100 - 0.04x} \\ Where\text{ x represents the yearly amount of club purchases} \\ and\text{ y is the yearly cost in dollars} \end{gathered}`

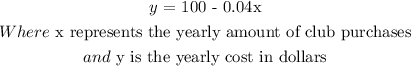
(a) The actual yearly cost of the membership if the club purchases for the year are 2100

Here we have:

x = 2100.

We find y using the equation above:

`\begin{gathered} y\text{ = 100 - 0.04 }*\text{ 2100} \\ =\text{ 16} \end{gathered}`

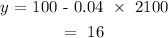
Answer : $16

(b) The amount of club purchases that would reduce the actual yearly cost of membership to $47

Here, we have:

y = $47

We find x using the equation above:

`\begin{gathered} 47\text{ = 100 - 0.04x} \\ Collect\text{ like terms} \\ 47-100\text{ = -0.04x} \\ -0.04x\text{ = -53} \\ Divide\text{ both sides by -0.04} \\ x\text{ = }(-53)/(-0.04) \\ x\text{ = 1325} \end{gathered}`

Answer: $1325

(c) The amount a member have to spend in yearly club purchases to reduce the yearly membership cost to $0

Here, we have y = $0

We find x using the equation:

`\begin{gathered} 0\text{ = 100 -0.04x} \\ Collect\text{ like terms} \\ -0.04x\text{ = 0-100} \\ -0.04x\text{ = -100} \\ Divide\text{ both sides by -0.04} \\ x\text{ = \$2500} \end{gathered}`

Answer: $2500