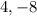Question

Identify the intercepts of the line: 6x -3y = 24

Answer 1

Consider that the intercept form of the equation of a line whose x-intercept is 'a' and y-intercept is 'b', is given by,

`(x)/(a)+(y)/(b)=1`

The given equation of the line is,

`6x-3y=24`

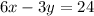
Transpose the terms to convert the equation in intercept form,

`\begin{gathered} (1)/(24)\cdot(6x-3y)=1 \\ (6x)/(24)-(3y)/(24)=1 \\ (6x)/(6\cdot4)-(3y)/(3\cdot8)=1 \\ (x)/(4)-(y)/(8)=1 \\ (x)/(4)+(y)/((-8))=1 \end{gathered}`

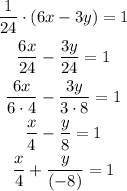
Comparing with the standard form,

`\begin{gathered} a=4 \\ b=-8 \end{gathered}`

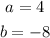
Thus, the x-intercept and y-intercept of the line, respectively, are

`4,-8`