Question

Write the standard form of the line that passes through the given points. Include your work in your final answer. Typeyour answer in the box provided to submit your solution.IP(6, 1) and (5, 4)

Answer 1

Given two points (6, 1) and (5, 4), what we can solve first is the slope of the line using the equation

`m=(y_2-y_1)/(x_2-x_1)`

Let x1 = 6, y1 = 1, x2 = 5, and y2 = 4. Solve for m, we get

`m=(4-1)/(5-6)=-3`

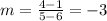
The point-slope form of a line is written in the equation as

`y-y_1=m(x-x_1_{})`

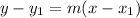
Substitute the values of y1, m, and x1 on the equation above, we get

`y-1=-3(x-6)`

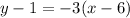
Simplifying the equation above, we arrive to the slope-intercept form of the equation

`\begin{gathered} y-1=-3x+18 \\ y=-3x+19 \end{gathered}`

To write this in standard form, let's put x and y on one side of the equation. We have

`3x+y=19`

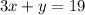
Therefore, the standard form of the line that passes through (6, 1) and (5, 4) is 3x + y = 19.