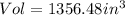Question

A cone with radius 12 inches and height 9 inches is shown. Enter the volume of the cone, in cubic inches. Round your answer to the nearest hundredth.

Answer 1

Step-by-step explanation:

Given;

We are given a cone with the following dimensions;

`\begin{gathered} radius=12in \\ height=9in \end{gathered}`

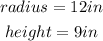
Required;

We are required to calculate the volume of the cone.

Step-by-step solution;

To calculate the volume of a cone, we use the following formula;

`\begin{gathered} Volume\text{ }of\text{ }a\text{ }cone: \\ Volume=\pi r^2(h)/(3) \end{gathered}`

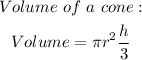
With the values provided, we can substitute and calculate as follows;

`Volume=3.14*12^2*(9)/(3)`
`Volume=3.14*144*3`
`Volume=1356.48`

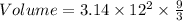
Rounded to the nearest hundredth, the volume is;

ANSWER:

`Vol=1356.48in^3`