Question

2x + 2y ≤ 0; (-1, -1), (1, 1)is each ordered pair a solution of the inequality

Answer 1

Only (-1,-1) is a solution to the inequality

Here, we want to test if the ordered pairs serve as a solution to the given inequality system

`2x\text{ + 2y}\leq\text{ 0}`

The way to be sure of this is to simply substitute the values

In the first set, we substitute -1 for x and -1 for y

We have;

`\begin{gathered} 2(-1)\text{ + 2(-1)} \\ =\text{ -4} \end{gathered}`

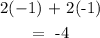
Since -4 is less than 0, we can conclude that the first pair is a solution to the inequality

We go on to try the second pair by making a substitution too

We have;

`2(1)\text{ + 2(1) = 4}`

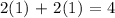
4 is greater than 0 and will not work for the given inequality as the question only considers values that are lesser than or equal to zero after substitution

So, only the first pair serves as a solution to the inequality