2)
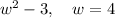
When we say that w = 4, it means that we can rewrite the expression and instead of "w", we will put "4", so
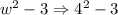
Now we have a numerical expression to solve, we can easily solve it!
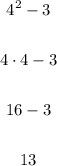
Therefore, the final answer is
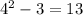
5)
Here we will do the same thing, the "hard" part is solving the numeric expression, it will be a little bit harder than the 2).
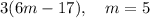
Again, repeat the same process, rewrite the expression, and instead of "m" you put "5"
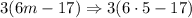
Again, another expression to simplify, remember that we always solve what is inside ( ) first, and we have a multiplication inside ( ) so we must solve it first

Now we solve the multiplication inside ( ) we can do the subctration
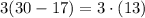
The last step is just to solve another multiplication
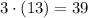
Now we simplified everything we can have the final answer:
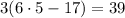
6)
Here we have a division, but it's similar with 5) and 2), we have
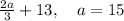
No secrets, repeat the process, but here, "a" will turn into "15", then
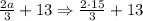
We can do the multiplication at the numerator of the fraction
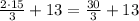
Now we can simplify the fraction, 30 divided by 3 is 10, then
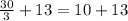
Now just do the sum and it's done!
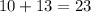
Hence the final answer is
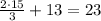
ANSWERS:
1) 43
2) 13
3) 67
4) 12
5) 39
6) 23