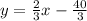Question

Find the equation of the line which passes through the point(5,-10) And is perpendicular to the given line express your answer in slope intercept form simplify your answer

Answer 1

Given the equation of a line, we can use the slope to find the slope of a perpendicular line. If we call m the slope, then the slope of a perpendicular line is:

`Slope\text{ }perpendicular\text{ }line=-(1)/(m)`

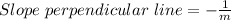
Now, we are given the equation of the line:

`(6x+2)/(4)-y=1-2y`

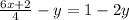
To find the slope, we need to rewrite this in slope-intercept form. To do this, we need to solve for y:

`\begin{gathered} (6x+2)/(4)=1-2y+y \\ . \\ (3)/(2)x+(1)/(2)=1-y \\ . \\ -((3)/(2)x+(1)/(2)-1)=y \\ . \\ y=-(3)/(2)x+(1)/(2) \end{gathered}`

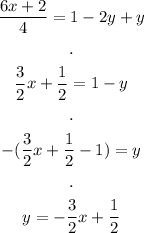
Then, the slope of this line is -3/2. The slope of a line perpendicular to it is the inverse of the reciprocal:

`Slope\text{ }perpendicular=-(1)/((-(3)/(2)))=(2)/(3)`

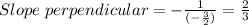
Now, we know that the slope of the line perpendicular is 2/3, and it must pass through the point (5, -10). We can use the slope- point fomr of a line.

The point-slope form of a line, given slope m and a point P is:

`\begin{gathered} P=(x_P,y_P) \\ . \\ y=m(x-x_P)+y_P \end{gathered}`

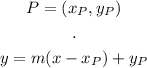
IN the perpendicular line, m = 2/3 and P = (5, -10):

`y=(2)/(3)(x-5)-10`

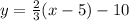
And solve:

`\begin{gathered} y=(2)/(3)x-(2)/(3)\cdot5-10 \\ . \\ y=(2)/(3)x-(10)/(3)-10 \\ . \\ y=(2)/(3)x-(40)/(3) \end{gathered}`

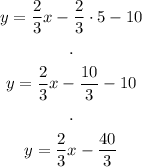
The answer is:

`y=(2)/(3)x-(40)/(3)`