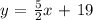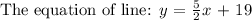
Step-by-step explanation:
The given point: (-6, 4)
slope of the line = 5/2
To get the equation of line in slope -intereot form, we will use the formula:
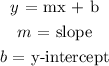
Since we already know the slope, we need to find the y-intercept
point (-6, 4): x = -6, y = 4
We will substitute the slope and the point in the formula above to get y-intercept:
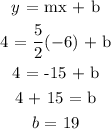
The equation of line in slope intercept becomes: