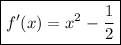Question

Find the derivative of each function. Simplify each derivative and express all exponents as positive values.

Answer 1

`\boxed{f^(\prime)(x)=x^2^{}-(1)/(2)}`

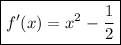
Step-by-step explanation:

Step 1. The function we have is:

`f(x)=(x^3)/(3)-(x)/(2)`

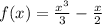
And we are asked to find the derivative of the function. The rule to find the derivative for this type of function is:

`\begin{gathered} \text{for a function }of\text{ the form} \\ f(x)=ax^n \\ \text{The derivative is:} \\ f^(\prime)(x)=a(n)x^(n-1) \end{gathered}`

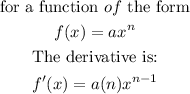
Step 2. Before we apply the derivative rule, remember the following:

`\begin{gathered} \text{for a function } \\ f(x)=g(x)+h(x) \\ \text{The derivative is:} \\ f^(\prime)(x)=g^(\prime)(x)+h^(\prime)(x) \end{gathered}`

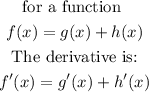
This means that we need to derivate each part or term of the function and combine them for the total derivative.

Step 3. Apply the derivative rule from step 1 to the given function.

First we rewrite the function as follows:

`\begin{gathered} f(x)=(x^3)/(3)-(x)/(2) \\ \downarrow \\ f(x)=(1)/(3)x^3-(1)/(2)x^1 \end{gathered}`

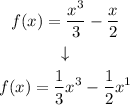
Apply the derivative rule:

`f^(\prime)(x)=(1)/(3)(3)x^(3-1)-(1)/(2)(1)x^(1-1)`

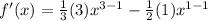
Step 4. The last step is to simplify the expression:

`\begin{gathered} f^(\prime)(x)=(1)/(3)(3)x^(3-1)-(1)/(2)(1)x^(1-1) \\ \downarrow \\ f^(\prime)(x)=(1)/(3)(3)x^2-(1)/(2)(1)x^0 \\ f^(\prime)(x)=x^2-(1)/(2)x^(^0) \\ \sin ce^{} \\ x^0=1 \\ \downarrow\text{ The result is }\downarrow \\ f^(\prime)(x)=x^2-(1)/(2) \end{gathered}`

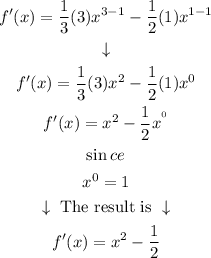
Answer:

`\boxed{f^(\prime)(x)=x^2^{}-(1)/(2)}`