Question

Graph a line with a slope of2that contains the point (-3,5).5

Answer 1

We will investigate how to graph a straight line on cartesian coordinate plane.

All equations of straight line are expressed in a general slope-intercept form as follows:

`y\text{ = m}\cdot x\text{ + c}`

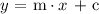
Where,

`\begin{gathered} m\colon\text{ slope} \\ c\colon\text{ y-intercept} \end{gathered}`

To graph any straight line we need the equation of the straight line or atleast two points that must lie on the line.

We are given the slope ( m ) and one of the points that lie on the line as follows:

`\begin{gathered} m\text{ = -}(2)/(5) \\ \\ (\text{ -3 , 5 )} \end{gathered}`

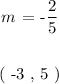
We need one another point that lies on the line to plot the graph of a straight line. To find another point we must completely express the equation of the straight line ( general form given above ).

We see that an equation of a straight line is defined by two parameters i.e ( m and c ). We are given the value of the slope ( m ). We will go ahead and plug it into the general slope-intercept form given above:

`y\text{ = -}(2)/(5)\cdot x\text{ + c}`

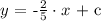
Now to determine the value of parameter ( c ) we must have atleast one point that lies on the line. We will use the point given to us and plug in the respective coordinates in the equation developed above and solve for ( c ) as follows:

`\begin{gathered} (\text{ x , y ) }\to\text{ ( -3 , 5 )} \\ \\ 5\text{ = -}(2)/(5)\cdot(-3)\text{ + c} \\ \\ 5\text{ = }\frac{5c\text{ + 6}}{5} \\ \\ 25\text{ = 6 + 5c} \\ \\ c\text{ = }(19)/(5) \end{gathered}`

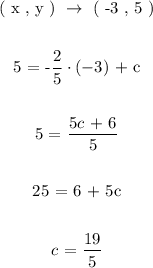
We will go ahead and update the equation of the straight line as follows:

`y\text{ = -}(2)/(5)\cdot x+(19)/(5)`

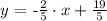
Now to get one more point to graph the plot we will assume any value of the for either variable ( x or y ) and then determine the value of the other variable as follows:

`\begin{gathered} x\text{ = 2} \\ \\ y\text{ = -}(2)/(5)\cdot(2)\text{ +}(19)/(5) \\ \\ y\text{ = }(-4+19)/(5) \\ \\ y\text{ = }(-15)/(5) \\ \\ y\text{ = -3} \end{gathered}`

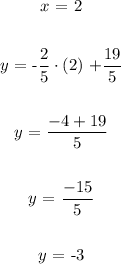
Therefore, we have the two points to plot the graph as follows:

`(\text{ -3 , 5 ) \& ( 2 , -3 )}`

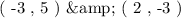
We can go ahead and select the above points on the given grid to construct the straight line!