Question

An ore cart of mass 1200 kg is rolling at a speed of 12.8 m/s across a flat surface a crane dumps 338 kg of ore into the cart from directly above it how fast does the cart move after being loaded with ore assume that frictional forces with the flat surface are negligible

Answer 1

Given,

The mass of the cart, M=1200 kg

The speed of the cart before the ore is dumped, u=12.8 m/s

The mass of the ore dumped on the cart, m=338 kg

From the law of conservation of momentum, the total momentum of the system of the cart and the ores before and after the ore is dumped into the cart must be equal.

Thus,

`Mu=(M+m)v`

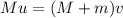
Where vis the speed of the cart after the ore is dumped.

On substituting the known values in the above equation,

`\begin{gathered} 1200*12.8=(1200+338)v \\ \Rightarrow v=(1200*12.8)/(1200+338) \\ =9.99\text{ m/s} \\ \approx10\text{ m/s} \end{gathered}`

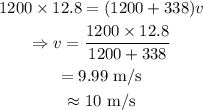
Thus the speed of the loaded cart will be 10 m/s