Question

The population of a certain city has been increasing exponentially accordingto the functionP (t) = 800, 000e0.051where t is the time in years (with t = 0 corresponding to 2014).a.) What was the population in the year 2014?b.) In what year will the population reach 1,200,000?c. what was the rate of change of the population in the year 2019?

Answer 1

`\begin{gathered} \text{ (a) }Given\text{ that p(t) = }800,000e^(0.05t) \\ \text{ In the year 2014, t=0} \\ \text{substitute t=0 into p(t) above} \\ p(0)\text{ = 800000}e^(0.05(0)) \\ p(0)\text{ = 800000}e^0 \\ p(0)\text{ = 800000}(1) \\ p(0)\text{ = 800000} \\ \text{The population at 2014 is 800,000} \end{gathered}`

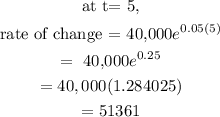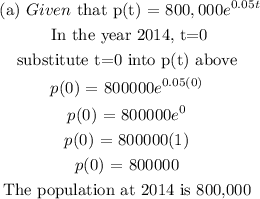
(b) To determine the year the population will reach 1,200,000, substitute p(t) = 1,200,000 into p(t) above and calculate the value of t

`\begin{gathered} \text{ p(t) = 1,200,000} \\ 1,200,000=800,000e^(0.05t) \\ \text{divide both sides by 800,000} \\ (1200000)/(800000)\text{ =}\frac{\text{ 800000}e^(0.05t)}{800000} \\ \\ 1.5=e^(0.05t) \\ \text{take }\ln \text{ of both sides} \\ \ln 1.5\text{ = }\ln e^(0.05t) \\ \ln 1.5=0.05t\ln e \\ \ln 1.5=0.05t(1) \\ \ln 1.5\text{ = 0.05t} \\ \text{divide both sides by 0.05} \\ (\ln 1.5)/(0.05)\text{ = t} \\ t=8 \end{gathered}`

The year when t= 8, given that t=0 in 2014 is the year 2022

(c) the rate of change of the population in the year 2019

Firstly, differentiate p(t) with respect to t

`\begin{gathered} p(t)\text{ = }800,000e^(0.05t) \\ \frac{\text{ dp}}{\text{ dt}}\text{ = 0.05(800,000)}e^(0.05t) \\ \frac{dp}{\mathrm{d}t}\text{ = 40,000}e^(0.05t) \\ \text{ This means that the rate of change of the function at any time t is 40,000}e^(0.05t) \\ \end{gathered}`

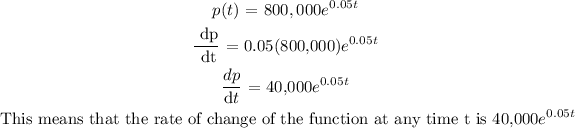
In the year 2019, t = 5

Substitute t=5 into the rate of change above

`\begin{gathered} \text{ at t= 5, } \\ \text{rate of change = 40,000}e^(0.05(5)) \\ =\text{ 40,000}e^(0.25) \\ =40,000(1.284025) \\ =51361 \end{gathered}`