Question

The half-life of radium is 1690 years. If 50 grams are present now, how much will be present in 800 years?

Answer 1

In order to determine the amount of radium after 800 years, use the following formula:

`N=N_oe^(-\lambda t)`

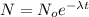
where,

N: amount of radium after t years = ?

No: initial amount of radium = 50g

λ: decay constant

t = 800

The decay constant is calculated by using the following expression:

`\lambda=(ln2)/(t(_1)/(2))=(ln2)/(1960)\approx3.5*10^(-4)`

where t1/2 = 1960 is the half-life.

Now, by replacing λ, No and t = 800 you obtain:

`N=50e^(-(3.5*10-4)(800))\approx37.68g`

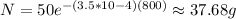
Hence, after 800 years there are approximately 37.68g of uranium